1 Tree
1.1 Definition
1.2 Operation
1.3 性能分析 & 计算相关问题
1.4 Implementation
1.4.1 二叉树的遍历
1.4.2 二叉搜索树的操作
2 Linked List
3 Stack & Queue
4 Heap
5 String
6 Hash今天,复习一下基本的数据结构。顺带解决一些小问题。
要解决的问题
BST的定义?key可以相等吗?
Binary Search Tree 与最小堆之间的区别?
完全二叉树等的概念歧义问题?
BST的平均高度?为什么?平均是什么意思?1 Tree
1.1 Definition
1.1.1 Tree 树
在计算机科学中,树是一种被广泛使用的数据结构/ADT,树模仿自然界中树的层次结构。
关于树的确切定义,可以使用递归的方式来定义。
即:(Recursive Defintion)
树是一些节点的集合。
这个集合可以是空集。
若非空,则一棵树由一个称作根root的节点,以及0个或者多个非空的子树构成。
这些子树中的每一棵都与root有一条边链接。
图1:一棵树的实例: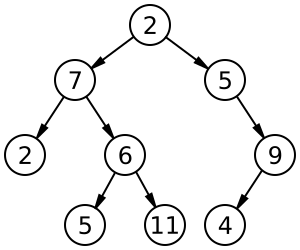
1.1.2 Binary Tree 二叉树
二叉树是一棵树,其中每个节点至多有两个儿子。
1.1.3 Binary Search Tree 二叉搜索树(BST)
二叉搜索是特殊的二叉树。 每一个有节点有一个Key键值。
对于树中的每个节点X,它的左子树中的所有Key<X.Key (≤X.Key).右子树中的所有Key>X.Key(≥X.Key)。
(关于上述两种不同的定义情况,其本质问题即使BST是否允许存在两个节点Key相等?)
这个我在不同的书中看到了不同的定义
[1]中给出的定义是不可以相等。
[2]中给出的定义是可以。即树中的每个节点X,左子树中的所有Key≤X.Key.右子树中的所有Key≥X.Key.
我个人认为:对于大部分情况而言,我们更倾向于不存在Key值相同的情况。这样即符合很多实际情况,又能够简化问题。
当然,也可以引入带有Key值相等的情况,这需要再实现上考虑这个问题。具体见[2]思考题12.1.
(而且[2]的算法皆是按照在不存在key值相等的情况下编写的) Binary Search Tree 与最小堆之间的区别:
二叉搜索树的节点的左右孩子是有序的,left.key < parent.key < right.key
而最小堆,其左右孩子是无序的,也没有大小关系。{left.key ,right.key}> parent.key
对于最小堆而言,查找最小值是O(1)的,由于其左右孩子无大小关系,其查找任意一key则是O(n)的。二叉搜索树与最优二叉搜索树:
最优二叉搜索🌲 动态规划1.1.4 其他Type的树
Perfect Binary Tree
A perfect binary tree is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.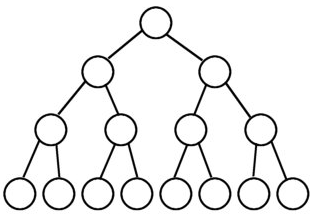
Full Binary Tree
每个节点的度为0或2 。
A full binary tree (sometimes referred to as a proper or plane binary tree)is a tree in which every node has either 0 or 2 children.
图2: A full binary tree
Complete Binary Tree
所有层全充满,除了最后一层。且最后一层的节点从左向右填充。
综上,即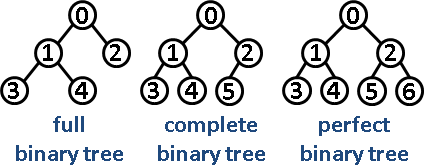
上述定义来自维基百科,此为最为广泛使用的定义。
然后不同的文献之间定义却存在歧义。主要在于完全二叉树的问题上。
譬如说,
在一些国外教程以及国内教材中【完全二叉树】一词指上图中的complete binary tree,而在算法导论中【完全二叉树】一词指上图中perfect binary tree。用【近似的完全二叉树】一词表示上图中的complete binary tree。
国内教材中
满二叉树 指 perfect binary tree
完全二叉树 指 complete binary tree
算法导论[2]中:
满二叉树 指 perfect binary tree
近似的完全二叉树 指 complete binary tree
完全二叉树 指 perfect binary tree知乎上有一个讨论此问题的问题为什么说“满二叉树也是完全二叉树?
同样的,对于树的深度depth和高度height不同的作者也都有不用的定义。
见:
What is the difference between tree depth and height?
link
另外,对于根节点的标记有的从0开始也有的从1开始。
先序序列为a,b,c,d 的不同二叉树的个数是
n个结点构成的不同二叉树个数为 c(n,2n)/(n+1) 【卡特兰数】
AVL树
why AVL?
对于BST而言,其查询插入删除的时间复杂度都是O(h),h为树的高度。
一个不好的消息是BST的最坏时间复杂是O(n)。即BST的高度最坏可以达到O(n),这也不难理解。 试想一颗总是朝着一个方向生长的二叉树。 它的高度便是O(n)。
为了提高性能,我们的出发点便是控制树高。 使得树高不至于那么高(O(n)级别)。
为了能够控制树高,我们期望树更加平衡些。即左右子树高度相差不是很大。
譬如说,我们可以限制对于任意一个节点,其左右子树的高度相等。这样的话,树的高度就会受限,不会疯狂的朝着一个方向生长。 然而这样的条件比较苛刻。 不容易满足。
于是我们可以限制每一个节点左子树和右子树的高度最多差1。这样的话既可以控制树高,又不是那么难以满足。
what ?
AVL树即平衡 二叉搜索树 其以发明者 Adelson-Velsky and Landis命名。
AVL 树 == BBST(Balanced Binary Search Tree)
一颗AVL树是其每一个节点左子树和右子树的高度最多差1的二叉搜索树。
AVL树是自平衡的,即使在插入删除操作中,它可以自己调整(Rotate)从而使得满足AVL树条件。
AVL树的每一个结点都有一个平衡因子Balanced Factor:为该结点的左子树的深度减去它的右子树的深度。
对于AVL树而言对于任一节点N,有BalanceFactor(N) ∈ {–1,0,+1}
AVL树的深度和logN是同数量级的(其中的N为结点个数) (why?)
Huffman树
如何构建?
性质
树中一定没有度为1的结点
ASL
huffman树与最优二叉搜索树的区别线索二叉树
前序和后序线索化之后,空链域为1
中序线索化后,空链域为2
n个结点的线索二叉树上含有的线索数为 2n - (n-1) = n+1
1.1.5 高级树结构
B 树
红黑树
基数树
Treap树
1.2 Operation 操作
- 二叉树
- 遍历 (前序/中序/后序/层次)
- 二叉搜索树BST
- 插入/删除
- 搜索
Note:
对于所有遍历操作,不论是递归实现还是迭代实现,其时间复杂度都是O(n)。 (why?)1.3 性能分析 & 计算相关问题
1.3.1 二叉树Binary Tree
对于遍历操作,不论是递归实现还是迭代实现,其时间复杂度都是O(n)。
1.3.2 二叉搜索树Binary Search Tree:
 [3]
[3]
对于插入,删除,查找操作其复杂度都是O(h) ,这是显而易见的。
接下来的问题便是h到底是多少,h与n的关系了.
对于树的深度而言,其
- 最坏深度为O(n) ,这是显而易见的。
- 平均深度 O(log n) 这导出两个问题,
- 1.为什么是O(log n)? 如何证明之
- 2.在这里平均的意义(含义)又是什么?
关于问题1,我在[1],[2]中找到了相关的说明。
[2] 中定理12.4 证明了
一颗有n个不同关键字的随机构建二叉搜索树的期望高度是O(log n )
NOTE:
在这里随机构建的含义即是,考虑n个不同的节点,其所有排列情况是n!中,对于每一种情形按次序依次插入一个元素构建BST,
注意只有插入操作,而没有删除操作。这样的构建过程叫做随机构建。
12.4节中同样证明了,一颗有n个不同关键字的随机构建二叉搜索树的期望高度是O(log n ) 。
但是对于既存在插入操作,又存在删除操作的BST,其平均深度在[2]中并未做说明。
If deletions are allowed as well as insertions,
"little is known about the average height of a binary search tree"[1] 中证明了,有n个节点,假设所有的树出现的机会相等时,则树平均深度为O(log n)
证明过程见下Weisss-p78
在这里,我认为其含义同[2],即随机构建,虽然[1]中貌似并未明确其平均含义。
对于既存在插入操作,又存在删除操作的情况下,
[1]中给出了如下结论:
已经证明,如果我们交替插入和删除θ(n^2)次,那么树的期望深度是θ(根号n)1.3.3 相关计算
设层数从1开始,即根节点为第1层,共有k层。
那么第i层,最多有2^(i-1)个节点。
整棵树,最多有2^0 + 2^1 + … 2^(k-1) = 2^k -1
若叶子节点即读书为0的节点有m个,度数为2的节点有n个,那么 m = n + 1
若整棵树有N个节点,设其高度为h。那么有[2^(h-1)-1] + 1 ≤ N ≤ 2^h - 1 即floor(log2(N)) + 1 后者ceil(log2(N+1))
1.4 Implementation 实现
1.4.1 Tree 遍历
1.4.2 二叉搜索树的操作
二叉树的重构
所谓重构即使,在不知道二叉树结构的情况下,从二叉树的先序中序后序遍历序列中重构出二叉树的结构。
可以证明:
采用 (先序遍历 || 后序遍历) + 中序遍历 可以重构出二叉树。
采用 先序遍历 + 中序遍历 不可以重构出二叉树
至于为什么?相关证明参见数据结构-二叉树重构
那么如何重构?
[1]: 数据结构与算法分析 C语言描述 Weiss
[2]: 算法导论 CLRS 3th Edition
[3] https://en.wikipedia.org/wiki/Binary_search_tree
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 rat_racer@qq.com

