Toaday I’m going to review some important sorting algorithms based on comparison.Besides,related data structures such as heap,priority queue will also be talked.
1 堆排序 && 优先队列
2 选择排序,插入排序,冒泡排序
3 快速排序
4 相关笔试题分析1 堆排序 && 优先队列
1 堆排序 && 优先队列
目录:
1.1 什么是堆? what and why?
1.1.1 what?
1.1.2 关于二叉堆 Binary Heap
1.1.3 why ?
1.2 堆的实现?什么二叉堆?
1.2.0 什么是二叉堆? binary heap?
1.2.1 堆的实现 二叉堆
1.2.2 斐波那契堆的实现
1.2.3 二项堆堆的实现
1.3 堆的相关操作? 堆排序?
1.3.1 Max-Heapify
1.3.2 Build-Max-Heap
1.3.3 HeapSort
1.3.4 关于优先队列の操作
1.4 堆的优缺点? 堆排序分析.
1.4.1 堆的优缺点
1.4.2 性能分析
1.5 优先队列 what and why? 堆与优先队列的关系?
1.5.1 什么是优先队列?Priority Queue
1.5.2 为什么是要使用优先队列? why?
1.5.3 Links between Heap and Priority Queue ?
1.6 优先队列的实现 性能分析?
1.6.1 Naive Implementation
1.6.2 Usual Implementation
1.6.3 Specialized Heaps Implementation
1.6.4 性能分析
1.7 Java,Python中的Heap,Priority Queue的实现
1.7.1 Java中的实现
1.7.2 Python中的实现
1.8 References & Externel Links
1.8.1 References
1.8.2 Externel LinksIn this Section,we’ll go deeply to reveal concrete definitions of Heap,Binary Heap,and Priority Queue and difference between them.
Basic Concepts and Methods will also be talked but not that specifically.
1.1 什么是堆?Heap?
1.1.1 what?
很多人以为
堆 == 二叉堆 == 优先队列 他们之间的关系真的是相等的吗? [Conclusion at section 1.5.3]
在英语中,heap作为动词 把..堆起/使成堆 的意思。作为名词是堆/很多的意思。
1964年,J. W. J. Williams 发明了堆排序(Heap Sort)[1],同时描述了如何利用二叉堆来实现一个优先队列。 使用该种数据结构可以高效的获取队列中的最大值或者最小值,从而进行排序操作。
(关于二叉堆见1.2,什么是优先队列见1.4 )
之后,后人不断加以改进,产生了一系列不同的堆.
比如k-叉堆,斐波那契堆,二项堆,左式堆,斜堆等等。 见堆变体。
从最初William的二叉堆用于堆排序,到后来的各式各样的堆,基本都是以树的形式表示。因此说
堆是一共基于树的数据结构。
维基百科也有说:A heap is a specialized tree-based data structure that satisfies the heap property。
所谓的heap property(堆的性质)即是大根堆/小跟堆的性质(所有父节点≥/≤子节点)。
因此,亦可以说堆不是一个数据结构,而是一类数据结构[this is my personal opinion]。
1.1.2 关于二叉堆 Binary Heap
二叉堆是一种堆。
维基百科上说:
A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues.[2]
显而易见的,将堆与二叉堆划等号(堆heap == 二叉堆bianry heap),显然是一个不成熟的想法。
heap != bianry heap,that is to say , heap is a class of data structures.but binay heap is a common type of heap.
它们与优先队列的关系将会在1.4中简要探讨。
1.1.3 why ?
既然知道了什么是堆,那么为什么要用堆呢?williams为什么要引入它呢。它又有哪些优点呢。
我认为,对于传统的大根堆或者小跟堆而言,最大值/最小值分别处于root节点位置.(为什么?)
这方便我们从中读/取最大值,最小值,这是一个O(logn)的操作。相对于数组而言,这有显著的性能提升。因此堆适用于那些需要频繁取最大/最小值的应用。
1.2 堆的实现?什么二叉堆?
堆采用树结构实现。对于不同的堆有不同的树实现。
1.2.0 什么是二叉堆
二叉堆是一种堆,二叉堆广泛地被使用,以至于,当我们谈论堆时,通常默认指的就是二叉堆。
二叉堆也是优先队列的一种常见的实现。 (什么是优先队列见1.4 )
二叉堆基于二叉树是实现,除了是二叉树之外,还需要满足下面两个条件。
1.Shape property :一个二叉堆是一个完全二叉树。在此含义即是所有的层(除了最后一层)都是满的,只有最后一层不是满的,而且最后一层的节点从左向右依次填充。
2.Heap property: (大根堆)对于所有的父亲节点而言,其值≥子节点。
(小根堆)对于所有的父亲节点而言,其值≤ 子节点。 【注意可以等于】
1.2.1 二叉堆的实现
对于最常见的二叉堆:
他使用二叉树来实现,这个二叉树是一个完全二叉树(完全二叉树在不同的文献中有着不同的含义,在此处我们取所有的层(除了最后一层)都是满的,只有最后一层不是满的,而且最后一层的节点从左向右依次填充。见维基百科-完全二叉树)
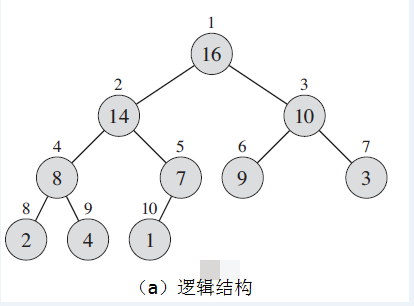
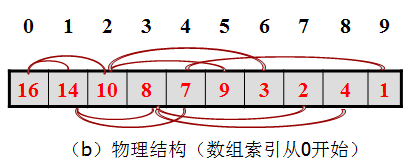
逻辑上,二叉堆是一棵树。 物理上,二叉堆常用数组来实现。而不需要指针。这样可以获得较好的性能。(考虑为什么可以?)
如下图所示:
逻辑结构:
物理结构:
1.2.2 斐波那契堆的实现
待续
1.2.3 二项堆的实现
待续
1.3 堆的相关操作? 堆排序?
对于不同的heap,我们有不同的操作,在此,我们先对最为广泛的二叉堆进行阐述。
【本部分主要采自算法导论第三版 && 只针对大根堆(小根同理)】
【注:大根堆 == 最大堆,小根堆 == 最小堆】
- Max-Heapify 维护大根堆的性质。O(log n)
- Build-Max-Heap 从无序的输入数据数组中构造一个大根堆。 O(n)
- HeapSort O(nlog n ) 对一个数组进行[原址]排序。
- Max-Heap-Insert,Heap-Extract-Max,Heap-Increase-Key,Heap-Maximum【O(1)】过程、时间复杂度均为O(log n )功能是利用二叉堆实现一个优先队列。
【此处只是列出了算法伪代码以及算法思想,比较晦涩,最好还是找到具体的例子(譬如算法导论上就可以找到),配合算法,会有更加深刻的理解,此处限于篇幅就不做举例了】
1.3.1 Max-Heapify
Max-Heapify(A,i) 自顶向下维护大根堆性质。 O(log n)
1.3.2 Build-Max-Heap
Build-Max-Heap(A) 从最后一个非叶子节点开始,到根节点一次调用Max-Heapify(A,i)
【此算法的复杂度是O(n) 而不是O(n log n)试想为什么?】【算法导论上有证明】
1.3.3 HeapSort
HeapSort(A) O(n log n )
思想:
每次从root节点取出最大值,然后调整。
即:
从最后一个节点开始,将其调换A[1]](最大值),将脱离堆,从根节点开始调整堆。
1.3.4 优先队列の操作
Max-Heap-Insert,Heap-Extract-Max,Heap-Increase-Key,Heap-Maximum【O(1)】过程、时间复杂度均为O(log n )功能是利用二叉堆实现一个优先队列。
these operations are implemented to implement a priority queue.
the operations above ,i.e. Max-Heapify,Build-Max-Heap ,HeapSort are enough for heapsort.
- Max-Heap-Insert,在大根堆中插入一个元素并调整之
- Heap-Extract-Max,取出最大值即根节点,然后调整之
- Heap-Increase-Key,将某个节点增加一定的值,然后调整之
- Heap-Maximum,返回根节点的值
1.4 堆的优缺点? 堆排序分析.
1.5 堆与优先队列的关系? 优先队列what and why?
1.5.1 什么是优先队列?Priority Queue
优先队列是一种类似于队列的数据结构。
熟悉数据结构的我们知道,队列是一种允许在一段进行插入(入队)以及另一端进行删除(出队)的数据结构。 它是一种FIFO类型的数据结构。 队列在很多方面都有很多应用,比如在cache(替换策略),进程/作业调度方面。
而,在很多情况下,我们需要考虑不同元素的优先权不同,譬如在操作系统调度中,有一种叫做SJF的算法(即最短作业有限),在此,优先级就是执行作业的用时长短。这种情况下,用基本的先入先出的队列就不能胜任了。
因此,引入了一种叫做优先队列(Priority Queue )的数据结构。
优先队列中的每一个节点都有对应的优先级。 在不同的应用中采用不同的指标作为优先级。
- 优先队列满足至少以下两种操作[4]
- Insert 插入/入队 将一个节点插入到优先队列
- Deelete Min/Max 删除最小值/最大值,或者称之为Min/Max出队.
- 其实可以将Stack,Queue作为优先队列的两种特殊情况(为什么?)
- 也可以将优先队列看做为队列的一种修改,当出队时,总是出优先级最大/小的节点。
1.5.2 为什么是要使用优先队列? why?
引入了优先队列,可以方便的执行插入以及取最大/最小值的操作。在很多应用中,这两种操作频繁出现。
- 我认为优先队列
- 一方面,其插入,取最大/最小值操作在很多应用中频繁使用,满足了这些应用的需求。
- 另一方面,使用堆来实现的优先队列具有很好的性能。这使得我们更加倾向于使用它们。(关于性能见1.5)
维基百科上列举了优先队列的一些重要应用[3]:
Bandwidth management
Discrete event simulation
Dijkstra's algorithm
Huffman coding
Best-first search algorithms
ROAM triangulation algorithm
Prim's algorithm for minimum spanning tree1.5.3 Links between Heap and Priority Queue ?
优先队列常使用堆Heap来实现,但是优先队列与堆在概念上是不同的。
优先队列是一种抽象数据结构ADT(逻辑上),它可以有很多实现(物理上),譬如堆,数组,链表等。
但是最常见且最高效的实现是采用堆来实现。
到目前为止,我们理清了三者之间的关系。
so 堆 != 二叉堆 != 优先队列 != 堆
Heap : 二叉堆,k-叉堆,二项堆,斐波那契堆,斜堆,etc..
PQ : Priority Queue(ADT) 。Many kinds of Implementations
二叉堆是堆的一种,常用于实现优先队列。
1.6 优先队列的实现 性能分析?
1.6.1 Naive Implementation
有很多非常simple的实现优先队列的方法,比如无序列表Unordered List。
尽管Simple,但是性能却不佳。对于无序列表而言,插入操作是O(1)的,出队Extract-Min/Max 却是O(n)的,因为要搜索整个列表。
1.6.2 Usual Implementation
为了提高性能,堆被引入作为实现。
普通的二叉堆具有O(log n )的performance for inserts and removals。
and O(n) to build initially。
普通二叉堆的变体,斐波那契堆, pairing heaps提供了更好的性能。
1.6.3 Specialized Heaps Implementation
有一些特殊的堆结构,可以提供附加一些的操作(除1.5.1中的两种),或者在一些特殊的数据类型上性能优于普通的堆。
见[3]
1.6.4 性能分析
下图为采用不同的堆作为优先队列时,相关操作的时间复杂度。【此为最小堆】

【采自维基百科,注释略之】
1.7 Java,Python中的Heap,Priority Queue的实现
1.7.1 Java中的实现
Class PriorityQueue
1.7.2 Python中的实现
heapq模块实现了二叉堆的功能,可以用来实现优先队列以及Heapsort。
为Min-Heap.且下标从0开始。
- API
- Heapify() 给定一List,原地 线性 将其变为最小堆。
- Heappop() 从堆中pop最小值,即索引[0]所在元素。
- Heappush() 向插入一个元素。
- 用例
- 此外还提供了
heapq.nlargest, heapq.nsmallest 用来返回n个最大/最小的元素。
实现HeapSort
def heapsort(iterable):
h = []
for value in iterable:
heappush(h, value)
return [heappop(h) for i in range(len(h))]
>>> heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
>>> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]实现优先队列
pq = [] # list of entries arranged in a heap
entry_finder = {} # mapping of tasks to entries
REMOVED = '<removed-task>' # placeholder for a removed task
counter = itertools.count() # unique sequence count
def add_task(task, priority=0):
'Add a new task or update the priority of an existing task'
if task in entry_finder:
remove_task(task)
count = next(counter)
entry = [priority, count, task]
entry_finder[task] = entry
heappush(pq, entry)
def remove_task(task):
'Mark an existing task as REMOVED. Raise KeyError if not found.'
entry = entry_finder.pop(task)
entry[-1] = REMOVED
def pop_task():
'Remove and return the lowest priority task. Raise KeyError if empty.'
while pq:
priority, count, task = heappop(pq)
if task is not REMOVED:
del entry_finder[task]
return task
raise KeyError('pop from an empty priority queue')最大堆的实现
待续
ref
1.8 References & Externel Links
1.8.1 References
[1] : Williams, J. W. J. (1964), “Algorithm 232 - Heapsort”, Communications of the ACM, 7 (6): 347–348
[2] :维基百科-二叉堆
[3] :维基百科-优先队列
[4] : 《数据结构与算法分析 C语言实现》 Weiss Chapter 6
1.8.2 Externel Links
Python使用heapq实现小顶堆(TopK大)、大顶堆(BtmK小)
1.2 选择排序,插入排序,冒泡排序
1.3 快速排序
1.4
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 rat_racer@qq.com